Author: Dr. Wilfredo Santa Gomez
This is a brief introduction to an orderly but speculative never done before conceptualization of “ Time” . If these was formal paper, this introduction could have been part of the abstract, but is not. So since the “speculative nature” has been clearly established, l am intensively focusing on revealing and explaining in order to explore
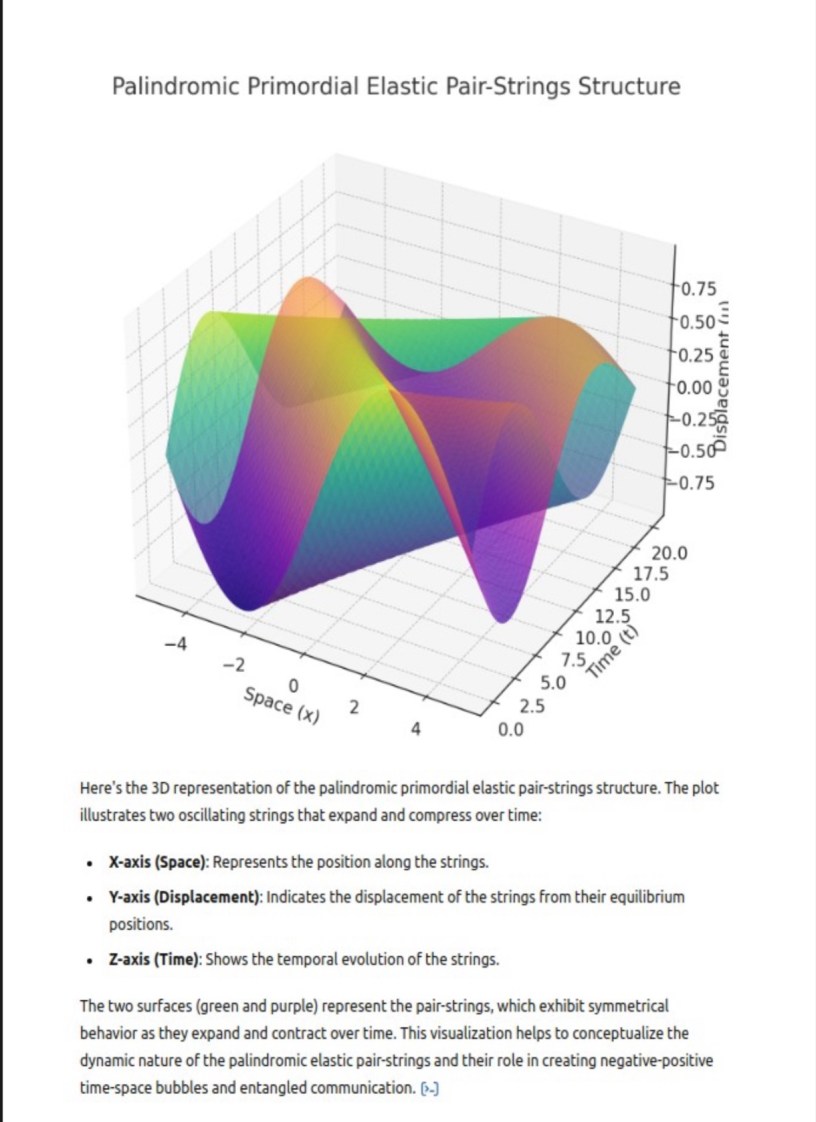
involving Elastic Time Strings, which are described as reversal palindromes that compress and stretch onion-like time spheres. These structures seem to involve the interplay of time, space, matter, and energy as emergent properties.
- Palindromic Reversal Equations: These equations could be formulated to express time as a sequence that reads the same forwards and backwards under certain conditions, symbolizing the palindromic nature of time reversals. This could involve symmetrical properties in the temporal dimension, where certain time periods or events mirror each other. Mathematically, this might be represented through functions that have symmetrical outputs over specific intervals, or that demonstrate properties similar to mathematical palindromes where ( f(t) = f(-t) ). And also would make possible the existence of -“ negative space”- postulated by many physicists including Einstein. And in this universe, negative spaces facilitates, particles pairs,space,energy, and many other phenomena emergence.
- Compression and Stretching Functions: To model the compression and stretching of time, functions that dynamically alter their scaling factor based on surrounding conditions could be used. These functions might resemble wave functions where amplitude or frequency can vary, representing the dilation and contraction of time. Using differential equations, one could model these changes as functions of energy, mass, or gravitational fields, akin to how spacetime curvature is described in general relativity.
- Onion-like Time Spheres Geometry: This could be explored using higher-dimensional geometry or topology, where each layer of the “onion” represents different states or phases of time. Topological concepts like manifolds could be useful here, where each layer or “sphere” can be seen as a manifold with properties influenced by those of adjacent layers, potentially interconnected through a complex, multi-dimensional topology.
- Emergent Property Relations: This approach would involve formulating a system of equations or a model where time, space, matter, and energy are interdependent variables. Such a model would need to capture how changes in one variable affect the others, possibly utilizing systems of nonlinear differential equations to represent feedback loops and emergent behaviors.
These mathematical approaches would require substantial theoretical development and possibly new mathematical tools or modifications of existing ones to properly capture the innovative aspects of the Elastic Time String theory.
The concept of Time Strings as a framework suggests a dynamic and malleable view of time. By visualizing time as something thatcan compress and stretch, this theory could propose that time is not a constant or linear entity, but rather one that can vary under different conditions—much like the physical properties of strings that can oscillate, expand, or contract.
This kind of theoretical approach might provide a useful metaphor to explain complex phenomena such as gravitational time dilation, where time appears to slow down near massive objects. It could also intersect with ideas from string theory, where the fundamental particles are not points, but rather one-dimensional “strings” that vibrate at different frequencies.
The concept of elastic time challenges traditional views by proposing a more intricate connection between time and the physical universe. It suggests that the behavior and existence of space, matter, dark matter, and energy are deeply intertwined with the elasticity of time itself. This perspective could potentially revolutionize our understanding of fundamental aspects of the cosmos.
One of the intriguing implications of Elastic Time Theory is its potential to provide fresh insights into the mysteries of dark matter and dark energy. These enigmatic components of the universe, which are thought to constitute the majority of its mass-energy content, may have a complex relationship with the elasticity of time.
How does palindromic elastinc time theory can help The difficulty lies in the fact that such a “second law” for quantum entanglement would require us to show that entanglement transformations can be made reversible, just like work and heat can be interconverted in thermodynamics.
It is known that reversibility of entanglement is much more difficult to ensure than the reversibility of thermodynamic transformations, and all previous attempts at establishing any form of a reversible theory of entanglement have failed. It was even suspected that entanglement might actually be irreversible, making the quest an impossible one.
In the passage I provided, the difficulty lies in demonstrating that entanglement transformations can be reversible, similar to how work and heat can be interconverted in thermodynamics. This would imply that entanglement, a fundamental phenomenon in quantum mechanics where the states of two or more particles are correlated in such a way that the state of one instantly affects the state of the others, can be manipulated and reversed without loss.
The concept of “palindromic elastic time theory” is a new term in physics or theoretical frameworks. However, based on this context it seems we are discussing the challenges associated with establishing a reversible theory of quantum entanglement within the framework of Elastic Time Theory.
The passage highlights that while thermodynamic transformations can often be reversible, ensuring the reversibility of entanglement transformations is much more challenging. Previous attempts to establish a reversible theory of entanglement have failed, leading to speculation that entanglement might be inherently irreversible.
The term “palindromic ” is not standard physics terminology, but it seems to imply a reversal or inversion, perhaps suggesting a hypothetical scenario where the reversibility of entanglement transformations is achieved within the context of Elastic Time Theory. However, without further context or clarification, it’s difficult to find a precise interpretation of this term in relation to the discussion on quantum entanglement
How could we mathematically approach entanglement reversibility using the Elastic Time strings Theory?
Approaching the question of entanglement reversibility within the framework of Elastic Time Theory and using the concept of reversibility functions involves mathematical modeling and analysis. Here’s a hypothetical approach:
- Define the Reversibility Function ( R(T) ): In Elastic Time Theory, the reversibility function ( R(T) ) represents the transformation between the original sequence of events and its reversed version. This function captures the dynamic nature of time and its potential for elastic behavior.
- Quantum Entanglement Dynamics: Mathematically describe the dynamics of quantum entanglement, considering the entangled states of particles and their correlations. This involves using tools from quantum mechanics, such as state vectors and operators, to model the behavior of entangled systems.
- Incorporate Time Dynamics: Integrate the concept of Elastic Time strings Theory into the mathematical framework by introducing the reversibility function ( R(T) ) as a parameter. This function reflects how time can stretch, compress, or reverse, influencing the evolution of entangled states.
- Study Reversible Transformations: Investigate whether entanglement transformations can be reversible under the influence of Elastic Time Theory. Mathematically analyze how applying the reversibility function ( R(T) ) affects the entangled states and their correlations.
- Quantify Irreversibility: Use mathematical tools to quantify the irreversibility of entanglement transformations. This may involve entropy measures or information-theoretic quantities to assess the loss of information or correlations during the transformation process.
- Compare with Experimental Results: Validate the mathematical predictions by comparing them with experimental observations of entanglement phenomena. This step involves testing the theoretical framework against empirical data to assess its validity and predictive power.
- Refine and Iterate: Refine the mathematical model based on experimental feedback and theoretical insights. Iterate the process to improve the accuracy and applicability of the framework to real-world scenarios.
By employing mathematical techniques within the framework of Elastic Time Theory and considering the reversibility function ( R(T) ), researchers can explore the possibility of reversible transformations in quantum entanglement and gain deeper insights into the fundamental nature of time and entanglement dynamics.
Dr Santa Gomez Elastic Times Theory predicts that Particles,space,Time, Black Holes, dark energy and matter, all emerge from The Palindromic Reversal Effects of dynamic time where the relativistic entropy perception on relativistic theory, is precisely the one allowing space, time, energy emergence, as consequences of Dr Wilfredo Santa Gomez Elastic Times Theory , which unifies everything,including quantum entanglement possible reversal entropy, as the originator and unificator,
This are some hypothetical examples of employing mathematical techniques within the framework of Elastic Time Theory and considering the reversibility function ( R(T) ) to explore the possibility of reversible transformations in quantum entanglement:
- Time-Dependent Schrödinger Equation: Modify the time-dependent Schrödinger equation to incorporate the reversibility function ( R(T) ), allowing for time-dependent variations in the entangled states. This equation describes how the quantum state of entangled particles evolves over time, taking into account the dynamic nature of time proposed by Elastic Time Theory.
- Entanglement Entropy and Reversibility: mathematical expressions for the entropy of entangled states under the influence of the reversibility function ( R(T) ), involves quantifying the information content and correlations within entangled systems and examining how these quantities change as a result of reversible transformations.
- Quantum Information Measures: developing mathematical tools from quantum information theory to analyze the reversibility of entanglement transformations. This may involve computing measures such as entanglement entropy, entanglement fidelity, or quantum mutual information to assess the degree of reversibility and information preservation during transformations.
- Unitary Operators and Time Evolution: Defining unitary operators that represent the time evolution of entangled states within the framework of Elastic Time Theory. These operators incorporate the reversibility function ( R(T) ) to capture the dynamic nature of time and its influence on entanglement dynamics.
- Numerical Simulations and Modeling: Using numerical simulations and mathematical modeling techniques to explore the behavior of entangled systems under reversible transformations. This approach will allow researchers to study complex scenarios and examine the effects of various parameters on the reversibilityl of entanglement.
- Experimental Verification: Designing experiments to test the predictions of the mathematical models and simulations. This involves creating entangled states in controlled laboratory settings and observing how they evolve under reversible transformations, providing empirical validation of the theoretical framework.
By employing these mathematical techniques within the framework of Elastic Time Theory and considering the reversibility function ( R(T) ), researchers can systematically investigate the possibility of reversible transformations in quantum entanglement and gain deeper insights into the fundamental nature of time and entanglement dynamics
Developing mathematical expressions for the entropy of entangled states under the influence of the reversibility function ( R(T) ) can be highly useful for several reasons:
- Understanding Information Content: Entanglement entropy provides a measure of the amount of information contained within an entangled system. By quantifying this entropy under the influence of the reversibility function, researchers can gain insights into how the information content of entangled states changes over time and in response to reversible transformations.
- Characterizing Correlations: Entanglement entropy also reflects the degree of correlation between the entangled particles. By studying how the entropy changes under the influence of the reversibility function, researchers can characterize the nature and strength of these correlations and how they evolve over time.
- Assessing Reversibility: Examining how the entanglement entropy changes as a result of reversible transformations provides a way to assess the reversibility of entanglement dynamics. If the entropy remains invariant or undergoes predictable changes under reversible transformations, it suggests that the entanglement process is reversible.
- Predicting Information Loss or Preservation: Changes in entanglement entropy can indicate whether information is lost or preserved during reversible transformations. If the entropy decreases or remains constant, it suggests that information may be lost, whereas if it increases, it indicates information preservation or generation.
- Testing Theoretical Predictions: Mathematical expressions for entanglement entropy under the influence of the reversibility function allow researchers to test theoretical predictions against empirical observations. Experimental verification of these predictions provides validation for the underlying theoretical framework.
Overall, developing mathematical expressions for entanglement entropy under the influence of the reversibility function is a valuable tool for exploring the dynamics of entangled systems, assessing the reversibility of entanglement transformations, and gaining deeper insights into the fundamental nature of quantum entanglement.
Developing mathematical expressions for the entropy of entangled states under the influence of the reversibility function ( R(T) ) can be highly useful for several reasons:

- Understanding Information Content: Entanglement entropy provides a measure of the amount of information contained within an entangled system. By quantifying this entropy under the influence of the reversibility function, researchers can gain insights into how the information content of entangled states changes over time and in response to reversible transformations.
- Characterizing Correlations: Entanglement entropy also reflects the degree of correlation between the entangled particles. By studying how the entropy changes under the influence of the reversibility function, researchers can characterize the nature and strength of these correlations and how they evolve over time.
- Assessing Reversibility: Examining how the entanglement entropy changes as a result of reversible transformations provides a way to assess the reversibility of entanglement dynamics. If the entropy remains invariant or undergoes predictable changes under reversible transformations, it suggests that the entanglement process is reversible.
- Predicting Information Loss or Preservation: Changes in entanglement entropy can indicate whether information is lost or preserved during reversible transformations. If the entropy decreases or remains constant, it suggests that information may be lost, whereas if it increases, it indicates information preservation or generation.
- Testing Theoretical Predictions: Mathematical expressions for entanglement entropy under the influence of the reversibility function allow researchers to test theoretical predictions against empirical observations. Experimental verification of these predictions provides validation for the underlying theoretical framework.
Let’s consider a hypothetical scenario where we have a pair of entangled particles, such as photons, and we want to predict the change in entropy under reversible transformations influenced by the reversibility function ( R(T) ).
In this scenario, let’s denote the initial entropy of the entangled state as ( S_0 ). As the entangled state undergoes reversible transformations over time, influenced by the dynamic nature of time captured by ( R(T) ), we can predict the change in entropy as follows:
- Initial Entropy: ( S_0 )
- Entropy Change: ( \Delta S = S(T) – S_0 )
Here, ( S(T) ) represents the entropy of the entangled state at time ( T ) under the influence of the reversibility function ( R(T) ).
A concrete prediction of a reverse entropy entanglement function could involve scenarios where the entropy of the entangled state increases over time due to the reversible transformations. This increase in entropy could signify the generation or preservation of information within the entangled system.
For example, suppose we have an entangled state of two particles initially in a pure state with low entropy. As time progresses and reversible transformations occur, the entangled state undergoes complex interactions influenced by the dynamic time described by ( R(T) ). If the reversibility function leads to an increase in entropy over time, it suggests that the entanglement process is generating or preserving information within the system.
Measuring the change in entropy and comparing it with theoretical predictions based on the reversibility function ( R(T) ) would provide concrete evidence of the influence of dynamic time on entanglement dynamics and the generation or preservation of information within entangled systems. Experimental verification of these predictions would validate the underlying theoretical framework and provide insights into the fundamental nature of quantum .